函数式编程

JavaScript是函数式语言吗

JavaScript 既不是 C++，Java 那样的纯面向对象语言，也不是 Haskell 和 Lisp 那样的纯函数式语言。

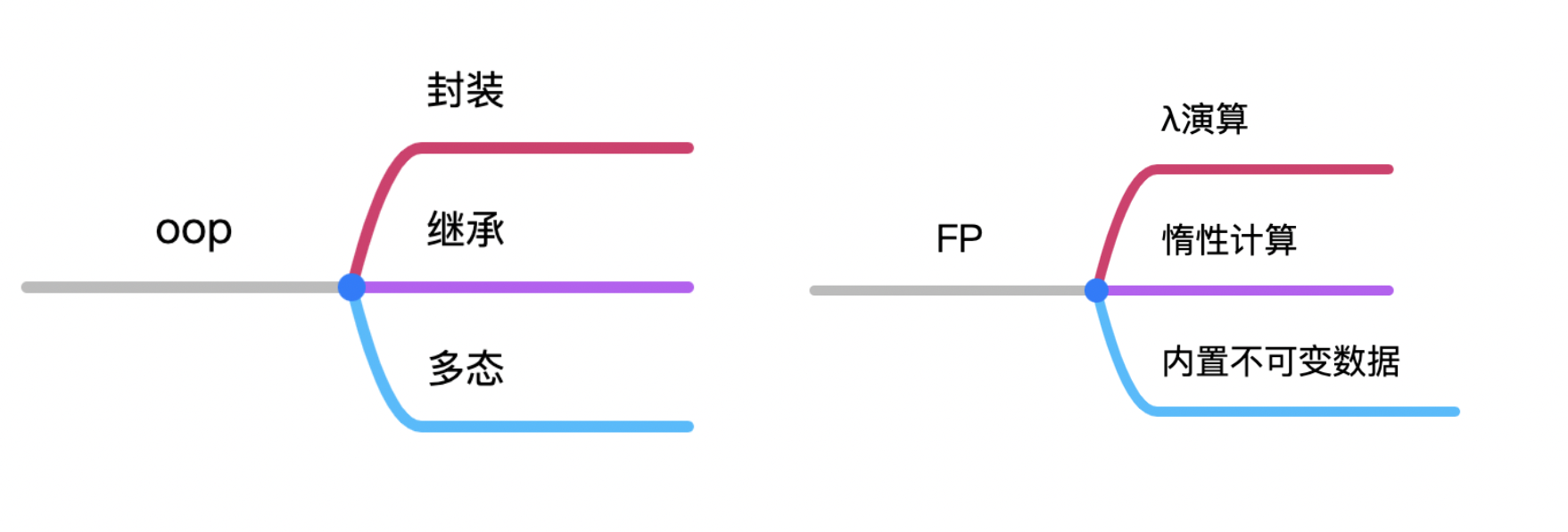
Js 可以通过某些方式来实现封装，继承，多态，函数重载，但其中面向对象的设计模式是通过原型对象来实现的，并不是真正的面向对象语言。

Js 允许匿名函数、高阶函数、闭包等函数式特性，且惰性计算可以通过 lazy.js 库实现，不可变数据可以简单地通过编程技术来实现，但这些都是需要程序员 polyfill，并不是语言本身所带的特性。

函数式编程定义

In computer science, functional programming is a programming paradigm where programs are constructed by applying and composing functions.

在计算机科学中，函数式编程是一种通过应用和组合函数来构建程序的编程范式。

编程范式

编程范式 指的是一种编程风格，它描述了程序员对程序执行的看法。在编程的世界中，同一个问题，可以站在多个角度去分析解决，这些不同的解决方案就对应了不同的编程风格。

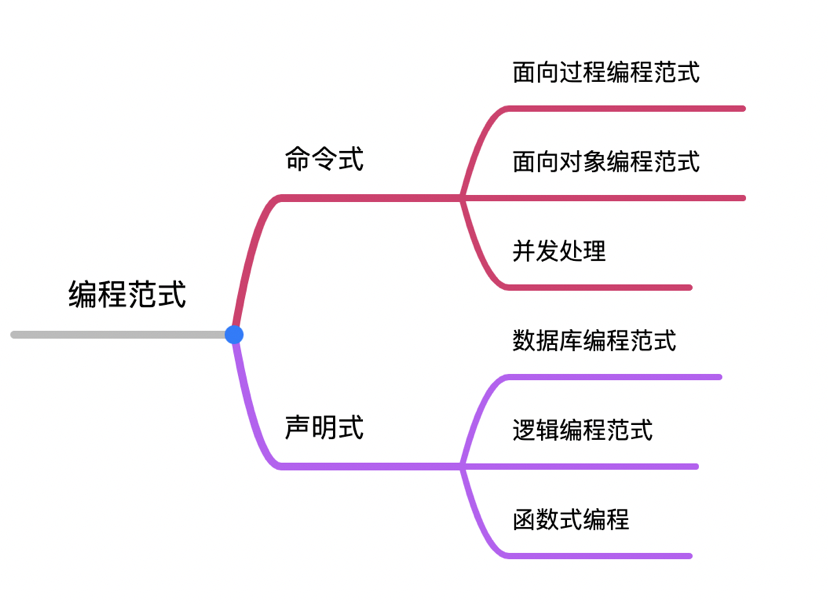
• Imperative 命令式：使用流程化的语句和过程直接控制程序的运行和数据状态。
• Declarative 声名式：定义计算的逻辑而不是定义具体的流程控制。

命令式，几乎完全集中于告诉计算机“如何”完成任务，它充斥着“if”语句、“for”循环、临时变量、带有副作用的函数调用以及函数之间的隐式数据流。当然，你可以通过它的逻辑来查看数据是如何流动和更改到最终状态的，但它一点也不清楚或直接。

声明式，它消除了前面提到的大多数命令式技术。注意没有显式的条件、循环、副作用。相反，它使用我们所说的函数式编程，如转换和组合。

函数式编程优势

• 代码精简
• 模块化
• 复用性
• 减少耦合
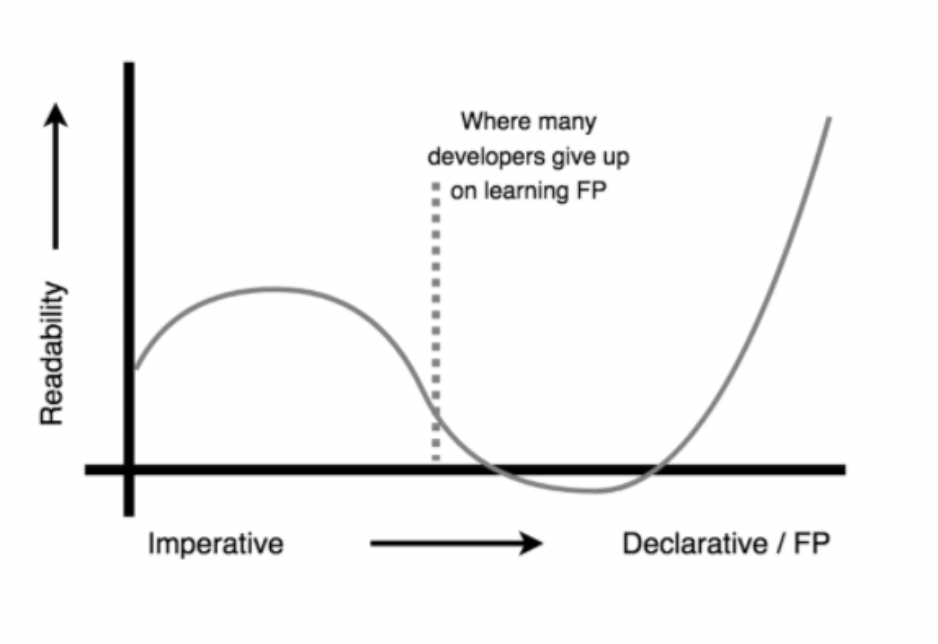
• 可读性

衍生应用场景

• 纯函数
• 记忆函数
• 递归与尾递归
• 高阶函数
• 闭包
• 函数柯里化
• 偏函数
• 函数组合
• 惰性求值

纯函数

纯函数（Pure Functions）是这样一种函数，即相同的输入，永远会得到相同的输出，而且没有任何可观察的副作用。这意味着对外部状态的解耦。

• 可缓存性（Cacheable）
• 可测试性（Testable）
• 合理性（Reasonable）
• 并行代码（Parallel Code）
• 可移植性／自文档化（Portable / Self-Documenting）

// slice 是纯函数，splice 不是
const arr = [1,2,3,4,5,6]
arr.slice(0,2) //[1,2]
arr.slice(0,2) //[1,2]

arr.splice(0,2) //[1,2]
arr.splice(0,2) //[3,4]

副作用

只要是跟函数外部环境发生的交互就都是副作用---这一点可能会让你怀疑无副作用编程的可行性。

• 发送一个 http 请求
• 获取用户输入
• DOM 查询
• 往数据库插入记录
• 打印/log
• …

函数式编程的哲学就是假定副作用是造成不正当行为的主要原因。

递归与尾递归

如何实现一个计算斐波那契数列的函数？

fibonacci：1，1，2，3，5，8，13 函数表达：f (n) = f (n - 1) + f (n - 2)

// 迭代
const fibonacci = n => {
  let current = 0;
  let next = 1;
  for (let i = 0; i < n; i++) {
    [current, next] = [next, current + next];
  }
  return current;
}

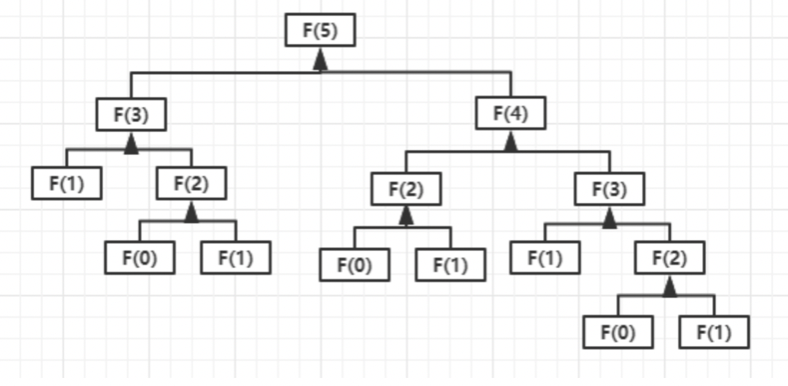
// 递归
const fibonacci = n => {
  return n < 3 ? 1 : fibonacci(n - 1) + fibonacci(n - 2);
}

递归的缺点：压栈和出栈会消耗性能。

// 尾递归
const fibonacci = (n, sum1 = 1, sum2 = 1) => {
  if (n < 3) return sum2;
  return fibonacci(n - 1, sum2, sum1 + sum2);
}

记忆函数

function memoize (fn) {
    let cache = {};
    return function () {
        let key = JSON.stringify(arguments);
        cache[key] = cache[key] || fn(...arguments); // 不必重新执行
        return cache[key];
    }
}
let fibonacciWithMemory = memoize(fibonacci);

fibonacciWithMemory(10);
fibonacciWithMemory(10);

函数经过记忆后运行的例子,可以明显的发现，第二次运行时是几乎不花时间的！

正是因为纯函数的可靠性，才能确保缓存的数据一定是我们想要的数据。

高阶函数

In mathematics and computer science, a higher-order function is a function that does at least one of the following:

• takes one or more functions as arguments (i.e. procedural parameters)
• returns a function as its result.

常见的高阶函数：

• map
• filter
• reduce
• every

// 模拟 map
const map = (array, fn) => {
    let res = []
    for (let i = 0; i < arr.length; i++) {
        res.push(fn(arr[i], i, arr))
    }
    return res
}

// 模拟 every
const every = (array, fn) => {
    let res = true
    for (let value of array) {
        res = fn(value)
        if(!res) break
    }
    return res
}
every(arr, v => v > 10)

// 模拟 some
const some = (array, fn) => {
    let res = false
    for (let value of array) {
        res = fn(value)
        if(res) break
    }
    return res
}

柯里化与偏函数

• 柯里化：把接受多个参数的函数变换成一系列接受单一参数的函数的技术。将一个 n 元函数转换成 n 个一元函数。
• 偏函数：一个函数，接受一个多参数的函数且传入部分参数后，返回一个需要更少参数的新函数。也就是将一个 n 元函数转换成一个 n - x 元函数。本质上可以将偏函数看成是柯里化的一种特殊情况。

优势：

• 对函数参数的缓存
• 让函数变得更灵活，让函数的粒度更小
• 把多元函数转换成一元函数，可以组合使用函数产生强大的功能

// arguments对象是所有（非箭头）函数中都可用的局部变量, 所以在这里需要在括号里声明一下 (...arguments)
const curry = (fn, ...args) => 
	args.length < fn.length
     ? (...arguments) => curry(fn, ...args, ...arguments)
	   : fn(...args)

function plus(a, b, c) {
  return a + b + c
}

let curryPlus = curry(plus)
curryPlus(1)(2)(3) // 6
curryPlus(1)(2,3) // 6
curryPlus(1,2)(3) // 6
curryPlus(1,2,3) // 6

let curryPlus = curry(plus, 1, 2, 3) 
console.log(curryPlus) // 6

柯里化在 Vue 源码中的应用

// src/platform/web/patch.js
function createPatch (obj) {
    // 这样就不必每次都patch参数里传 obj 了
    return function patch (vdom1, vdom2) {
        ..
    }
}

const patch = createPatch(...)

函数组合

洋葱代码：tOUpper(first(reverse(arr))

可以用函数组合把细粒度的函数组合成一个新的函数

function compose(...args) {
    return function(value) {
        return args.reverse().reduce((acc, cur) => cur(acc), value)
    }
}

// 实现：数组中的字符串 reverse -> 取第一个 -> 转换为大写
function reverse (arr) {
  return arr.reverse()
}
function first (arr) {
  return arr[0]
}
function toUpper(str) {
  return str.toUpperCase()
}

const f = compose(toUpper, first, reverse)
console.log(f(['one', 'two', 'three'])) // THREE

Pointfree 编程风格：即不使用所要处理的值，只合成运算过程。

惰性计算

lazy.js

惰性计算，也称为非严格计算，按需调用和延迟执行，是一种计算策略，它等待直到需要值才能计算函数的结果，这对函数编程特别有用。

Lazy([1,2,3,4,5,6,7,8,9,10])
	.map(i => i * 2)
	.filter(i => i <= 10)
	.take(3)
	.each(i => print(i))

// 2, 4, 6

理论范畴

对于函数式编程来说，以下这些理论不是必要的，其实你不懂也可以学会函数式编程，作为了解在这里简单介绍下。

• Category theory 范畴论
• Morphisms 态射
• Functors 函子
• Monads 单子
• Semigroup 半群
• Monoid 幺半群

范畴

任何事物都是对象，大量的对象结合起来就形成了集合，对象和对象之间存在一个或多个联系，任何一个联系就叫做态射。

函子

函子是一个容器，具有 map 方法，可以映射到另一个容器。

自函子：自函子就是一个将范畴映射到自身的函子。

单子

自函子范畴上的一个幺半群

幺半群

定义一：对于非空集合 S，若在 S 上定义了二元运算 ○，使得对于任意的 a, b ∈ *S,*有 a ○ b ∈ S，则称 {S, ○} 为群。

定义二：若 {S, ○} 为广群，且运算 ○ 还满足结合律，即：任意 a, b, c ∈ S，有 (a ○ b) ○ c = a ○ (b ○ c)，则称 {S, ○} 为半群。

定义三：幺半群是一个存在单位元（幺元）的半群。单位元：对于半群 <S, ○>，存在 e ∈ S，使得任意 a ∈ S 有 a ○ e = e ○ a

函子

class Functor {
  static of (value) {
    return new Functor(value);
  }
  constructor (value) {
    this._value = value;
  }
  map (fn) {
    return Functor.of(fn(this._value));
  }
}

// 链式操作，且不直接操作值
Functor.of(5).map(add5).map(double)

• 函子是一个容器，里面包含了值。

• 容器具有map方法。该方法将容器里面的每一个值，映射到另一个容器。

• 函子具有有of方法，用来生成新的容器。

• 运算都是通过函子完成，不直接针对于值。

Maybe 函子

// 如何处理初始值为空的情况
Functor.of(null).map(s => s.toUpperCase());

class Maybe {
  static of (value) {
    return new Maybe(value);
  }
  constructor (value) {
    this._value = value;
  }
  map (fn) {
    return this._value ? Maybe.of(fn(this._value)) : Maybe.of(null);
  }
}

Ethier 函子

// 如何实现以下功能
function addOne (x) {
  return x + 1;
}

Functor.of(5, 6).map(addOne); // Functor(5, 7)
Functor.of(1, null).map(addOne); // Functor(2, null)

class Ethier {
  static of (left, right) {
    return new Ethier(left, right);
  }
  constructor (left, right) {
    this.left = left;
    this.right = right;
  }
  map (fn) {
    return this.right 
      ? Ethier.of(this.left, fn(this.right)) : Ethier.of(fn(this.left), this.right);
  }
}

单子

• 函数嵌套我们可以通过 compose 来解决。

• 函子嵌套我们可以通过 Monads 来解决。

class Monad {
  static of (value) {
    return new Monad(value);
  }
  constructor (value) {
    this._value = value;
  }
  map (fn) {
    return Monad.of(fn(this._value));
  }
  join () {
    return this.value;
  }
}

const a = Monad.of(Monad.of('str'));
a.join().map(toUpperCase);

易与不易

• 易：生生之谓易。“落花流水春去也”，这是根本性的规律，人们只有知道如何去适应这种变化的艺术，才不会被社会给淘汰。
• 不易：老子称之为：有物混成，先天地生，寂兮寥兮，独立而不改，周行而不殆。庄子称之为“有情有信，无为无形，可传而不可受，可得而不可见，自本自根，未有天地，自古以固存……先天地生而不为久，长于上古而不为老”。

变易：世界上的万事万物包括天地在内，都不是一成不变的，每一分钟都在悄悄的改变着现实的情况，只是有些变化显著，可以被人们所见到，而有些变化缓慢，并不被人们所察觉。

不易：天地之间万事万物都会改变，可是却有一个永远不变的东西存在，他是万事万物的本源，是永恒的存在。很多人都会感慨“世事无常”，觉得自己好像什么都掌握不住。这世上的变，变的只是现象而已，变的背后一定有不变的东西。所以说不易，就是万事万物背后的规律，背后不变的常则，我们把它叫做“常”，哲学上叫做“本体”。

面向对象编程有两个概念，对象和类。他们是什么？是变化的中间态，个体，实体，张三是一个对象，李四又是一个对象，这是无穷无尽的。

易经里的那个不易，不变，就好比函数式编程，函数具有不变性，一致性。就比如纯函数，一点副作用都没有。所有的变化，最后都通过函数串了起来。而变化的后面，就是不变，以不变应万变。我觉得这就是函数式编程的精髓！

参考资料

JavaScript中的函数式编程 (opens new window)

JavaScript轻量级函数式编程 (opens new window)