# 北大肖臻老师《区块链技术与应用》公开课学习 5
- 学习地址:https://www.bilibili.com/video/BV1Vt411X7JF (opens new window)
- 参考文章:北京大学肖臻老师《区块链技术与应用》公开课笔记15——ETH概述篇 (opens new window)
# ETH 概述
BTC 和 ETH 为最主要的两种加密货币,BTC 称为区块链 1.0,以太坊称为区块链 2.0。因为了比特币设计中存在某些不足,以太坊便对其进行了改进。例如:
- 出块时间: 以太坊出块时间降低到十几秒,以及设计了一套共识协议
mining puzzle:BTC挖矿属于计算密集型,挖矿设备专业化(ASIC),以太坊设计的mining puzzle对内存要求高,限制了ASIC的使用(ASIC resistance)- 未来,以太坊还将会用权益证明(proof of stake)替代工作量证明(proof of work)
- 此外,以太坊增加了对智能合约(smart contract)的支持。
# 为什么智能合约
BTC 本身是一个去中心化的货币,在比特币取得成功之后,很多人就开始思考:除了货币可以去中心化,还有什么可以去中心化?以太坊的一个特性就是增加了对去中心化的合约的支持。
- BitCoin: decenralized currency, BTC, 最小单位一聪
- Ethereum: decenralized contract, ETH, 最小单位一
wei
货币本身由政府发行,政府公信力为其背书,BTC 通过技术手段取代了政府的职能。
现实生活中,我们经常提到 契约 或 合约。合约的有效性也是需要政府进行维护的,如果产生纠纷需要针对合法性合同进行判决(打官司)。ETH 的设计目的就是,通过技术手段来实现取代政府对于合约的职能(区块链的不可篡改性)。并不是所有的合同都可以实现,比较简单的可以使用智能合约。
智能合约有什么好处?
去中心化的货币的好处是跨国转账,比法币快很多。 智能合约: 若合同签署方并非一个国家,没有统一的司法部门。如果可以编写无法修改的合约,所有人只能按照相关参与方执行,无法违约。
# ETH 账户
BTC 系统是基于交易的账本,系统中并未显示记录账户有多少钱,只能通过 UTXO 进行推算。这种隐私保护比较好,但是使用起来比较别扭。比如 A 转给 B 比特币的时候,A 需要说明币的来源。但是我们实际中存钱说明来源,花钱则不用。此外,BTC 账户中的钱在花的时候,必须一次性全部花出去。
A => B(10BTC) B => C(3BTC) 如果 B 只转给 C 3个 BTC,那么剩下的 7个 BTC 将作为交易费给矿工,所以还要将剩下的钱转给自己:B => B'(7 BTC) 比特币系统中没有显式的基于账户的模型 而以太坊系统则采用了基于账户的模型,与现实中银行账户相似。
优点:转账是否合法只需要查看转账者账户中以太币是否足够即可,同时也不需要每次全部转账,这也天然地防范了双花攻击。(你要是花两次我就从你账户扣两次钱)
缺点:重放攻击:A 向 B 转账,过一段时间,B 将 A 的交易重新发布,从而导致 A账户被扣钱两次。
为了防范重放攻击,给账户交易添加计数器记录该账户交易过多少次,转账时候将转账次数计入交易的内容中。 系统中全节点维护账户余额和该计数器的交易数,从而防止本地篡改余额或进行重放攻击。 交易内容:A => B(10ETH)、nonce = 21(这是第21次交易)、Signed by A 如果重放上述交易内容,会发现 nonce = 21 的交易已经被发布了,就不会执行了。
以太坊系统中存在两类账户:外部账户和合约账户。
- 外部账户:类似于
BTC系统中公私钥对。存在账户余额balance和计数器nonce - 合约账户:并非通过公私钥对控制。合约账户不能主动发起交易,只能接收到外部账户调用后才能发起交易或调用其他合约账户。其除了
balance和nonce之外还有code(代码)、storage(相关状态-存储)
创建合约时候会返回一个地址,就可以对其调用。调用过程中,代码不变但状态会发生改变。
# 为什么以太坊要基于账户的模型
比特币隐私保护比较好,支持每次交易都更换账户。但以太坊是为了支持智能合约,而合约签订双方是比较稳定的身份且较少变化的。尤其是对于合约账户来说,需要保持稳定状态。
# ETH 状态树
首先,我们要实现从账户地址到账户状态的映射。在以太坊中,账户地址为 160字节 ,表示为 40个16进制。状态包含了余额(balance)、交易次数(nonce),合约账户中还包含了代码(code)、存储(stroge)。
直观地来看,其本质上为 key-value 键值对,所以直观想法便用哈希表实现。若不考虑哈希碰撞,查询直接为常数级别的查询效率。但采用哈希表,难以提供 Merkle proof
- 我们能否像
BTC,将哈希表的内容组织为Merkle Tree?
当新区块发布,哈希表内容会改变,再次将其组织为新的
Merkle Tree。如果这样,每当产生新区块(ETH中新区块产生时间为10s左右),都要重新组织Merkle Tree,很明显这是不现实的。 需要注意的是,比特币系统中没有账户概念,交易由区块管理,而区块包含上限为4000个交易左右,所以Merkle Tree不是无限增大的。而ETH中,Merkle Tree来组织账户信息,很明显其会越来越庞大。 实际中,发生变化的仅仅为很少一部分数据,我们每次重新构建 Merkle Tree 代价很大
- 那我们不要哈希表了,直接使用
Merkle Tree把所有的账户都放进去,每次修改只需要修改其中一部分即可,这个可以吗?
实际中,
Merkle Tree并未提供一个高效的查找和更新的方案。此外,将所有账户构建为一个大的Merkle Tree,为了保证所有节点的一致性和查找速度,必须进行排序。
- 不排序有什么问题?
Merkle Tree的叶子节点是账户信息,如果不排序,系统中有很多全节点会按照自己的排序方式进行构造账户信息,导致Merkle Tree均不相同,根哈希值也不同。
- 比特币的
Merkle Tree不也没排序吗?
比特币每个全节点收到的交易顺序也是不一致的,
Merkle Tree根哈希值也不一样。但是比特币是每个节点在本地组装一个候选区块,它自己决定收集哪些交易,然后去挖矿争夺记账权,只有挖到矿的人才能决定发布区块,这个顺序是唯一的。
- 那么经过排序,使用
Sorted Merkle Tree可以吗?
新增账户,由于其地址随机,插入
Merkle Tree时候很大可能在Tree中间,必须进行重构。所以Sorted Merkle Tree插入、删除的代价太大。
# MPT
以太坊采取的数据结构:MPT,首先介绍一下 trie 前缀树(字典树)
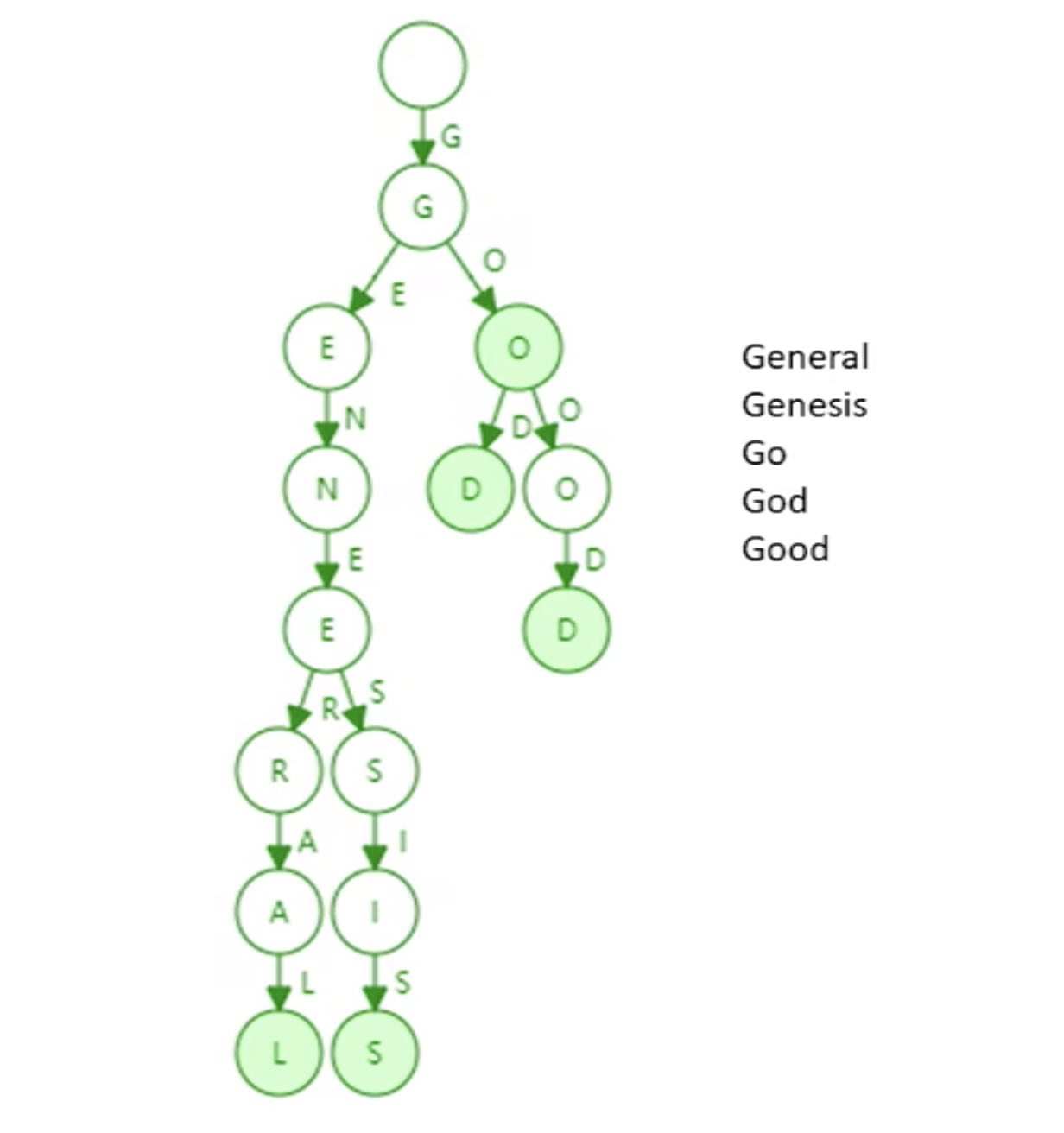
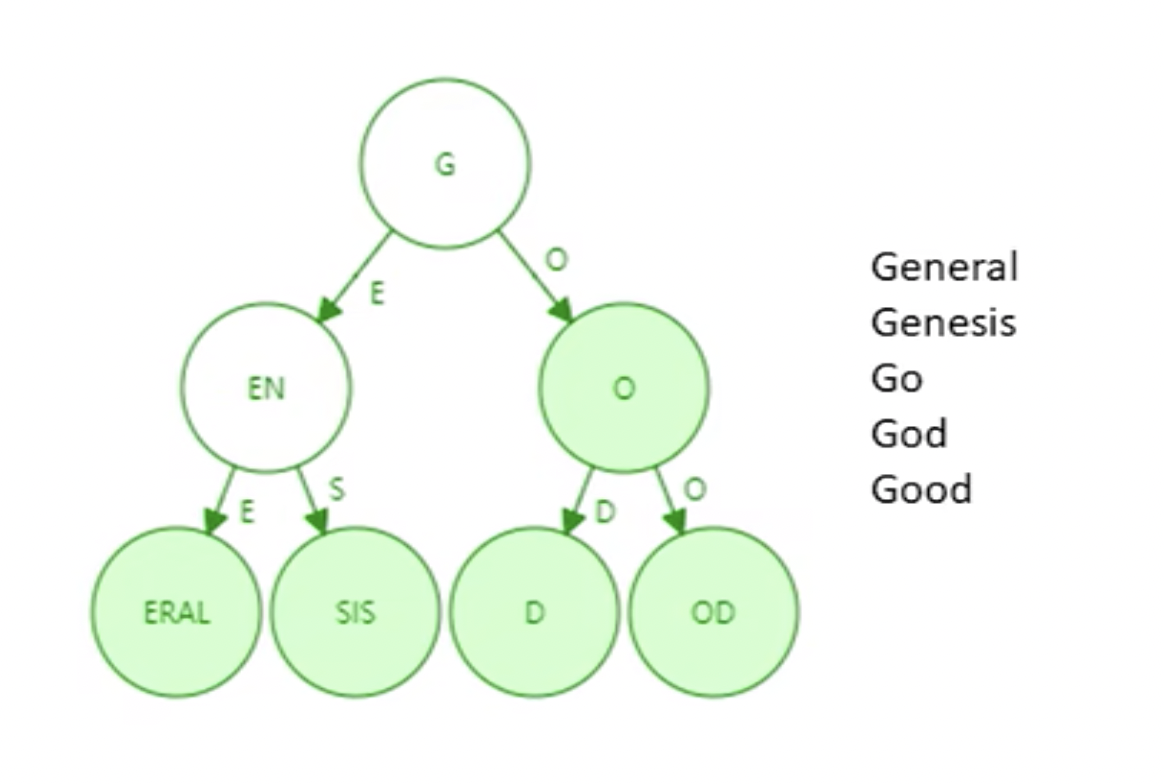
trie中每个节点的分支数目取决于每个元素的取值范围(图例中最多26个英文字母分叉+1个结束标志位)。以太坊中是16进制表示(0 ~ f)加上一个结束标识符为17个分叉。trie查找效率取决于key的长度。实际应用中(以太坊地址长度为160字节)。trie上面不会发生哈希碰撞,两个账户的地址不一样,映射到trie一定是不同的分支。- 给定输入,无论如何顺序插入,构造的
trie都是一样的。 - 更新的局部性比较好:每次发布一个区块,系统中绝大多数账户的状态是不变的,只有个别才会变,所以更新操作的局部性很重要。
trie上只需要遍历某一个分支,并不需要遍历整棵树。 - 缺点:存储上会有浪费,很多节点只有一个子节点。因此引入了
Patricia tree/trie(经过路径压缩后的前缀树)。
需要注意的是,如果新插入单词,原本压缩的路径可能需要扩展开来。什么情况下路径压缩效果较好?树中插入的键值分布较为稀疏的情况下,路径压缩效果较好。看以下例子:
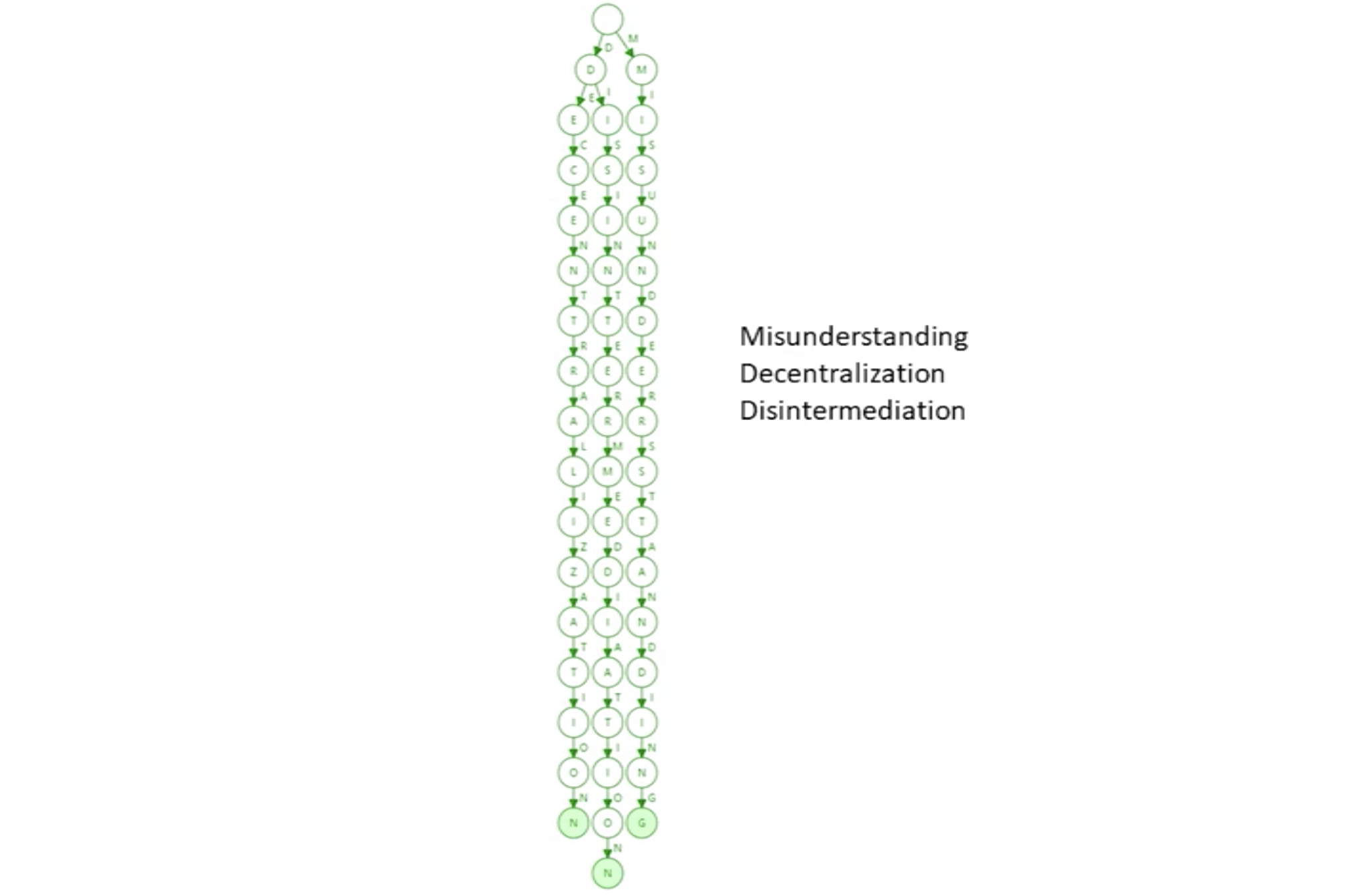
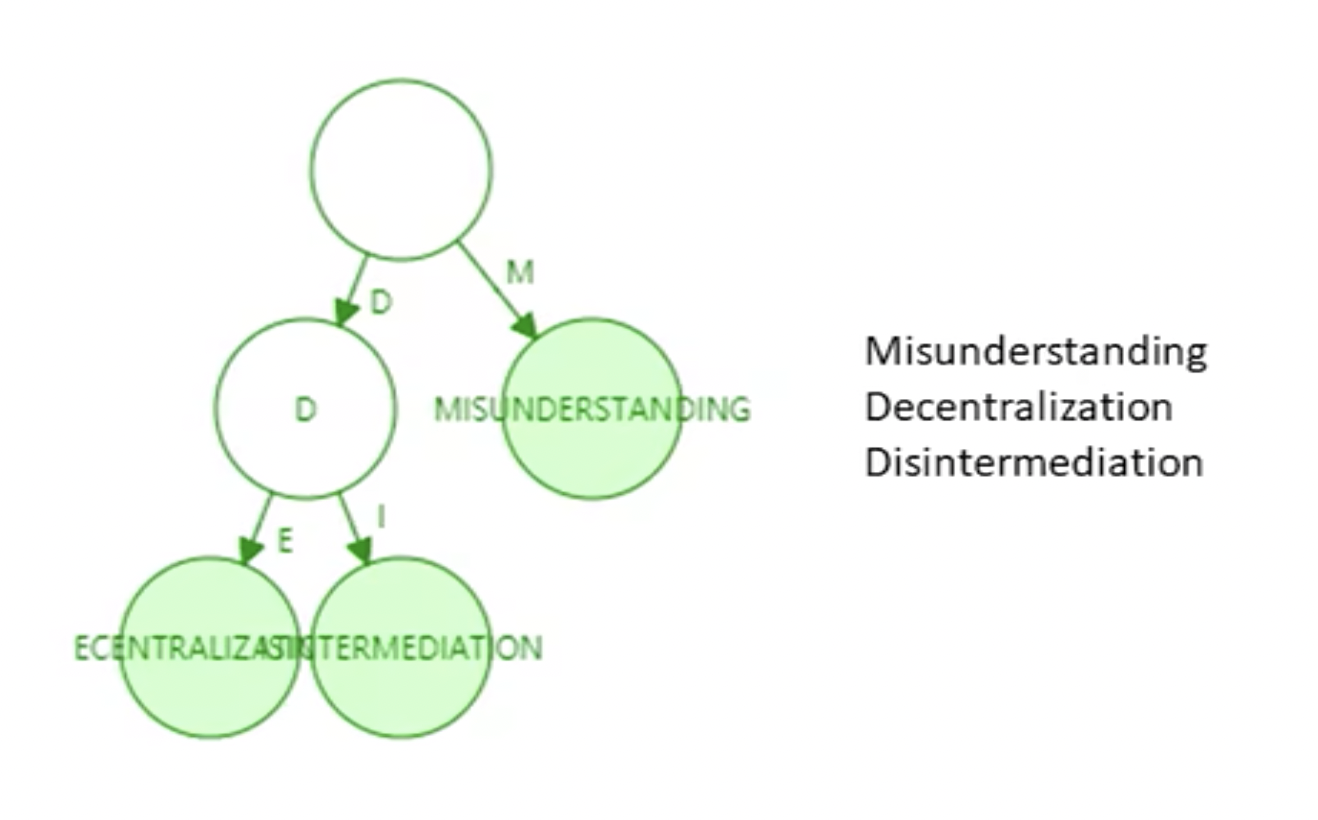
在以太坊系统中,160 位的地址存在 2^160 种,以太坊全世界的账户数加一起也远不足这个数,为什么地址搞的这么稀疏呢?
就是因为地址分布稀疏,所以路径压缩效果较好。 以太坊创建账户在本地创建即可,类似于比特币,那么会不会两个创建的账户地址一样呢?有可能,但是比地球爆炸的可能性还要低,就是因为地址足够长,足够稀疏。 实际上,在以太坊种使用的并非简单的
Patricia tree,而是MPT(Merkle Patricia tree)
MPT 就是将所有账户组织为一个经过路径压缩和排序的 Merkle Tree (指针为哈希指针),其根哈希值存储于 block header 中。根哈希值的用处:
- 防止篡改。
- 提供
Merkle proof,可以证明账户余额,轻节点可以进行验证。 - 给一个账户转账之前,证明某个发生了交易的账户是否存在。
以太坊中针对 MPT 进行了修改,我们称其为 Modified MPT。
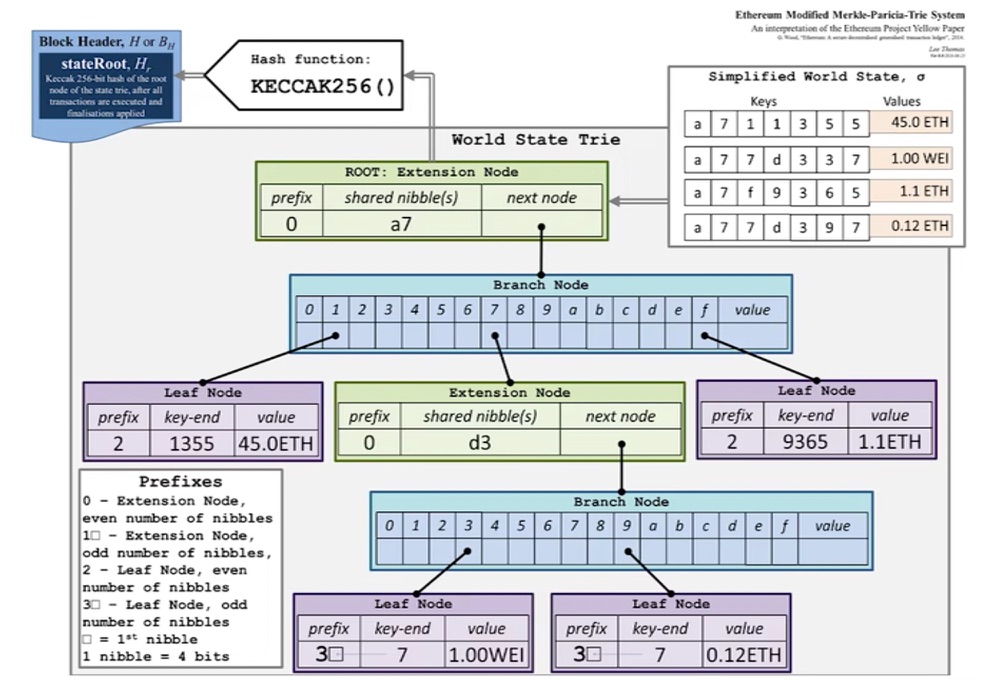
- shared nibble(s):十六进制
- extension node:扩展节点,经过路径压缩的节点
- leaf node:叶子节点
- branch node:分支节点
每次发布新区块,状态树中部分节点状态会改变。但改变并非在原地修改,而是新建一些分支,保留原本状态。如下图中,仅仅有新发生改变的节点才需要修改,其他未修改节点直接指向前一个区块中的对应节点。
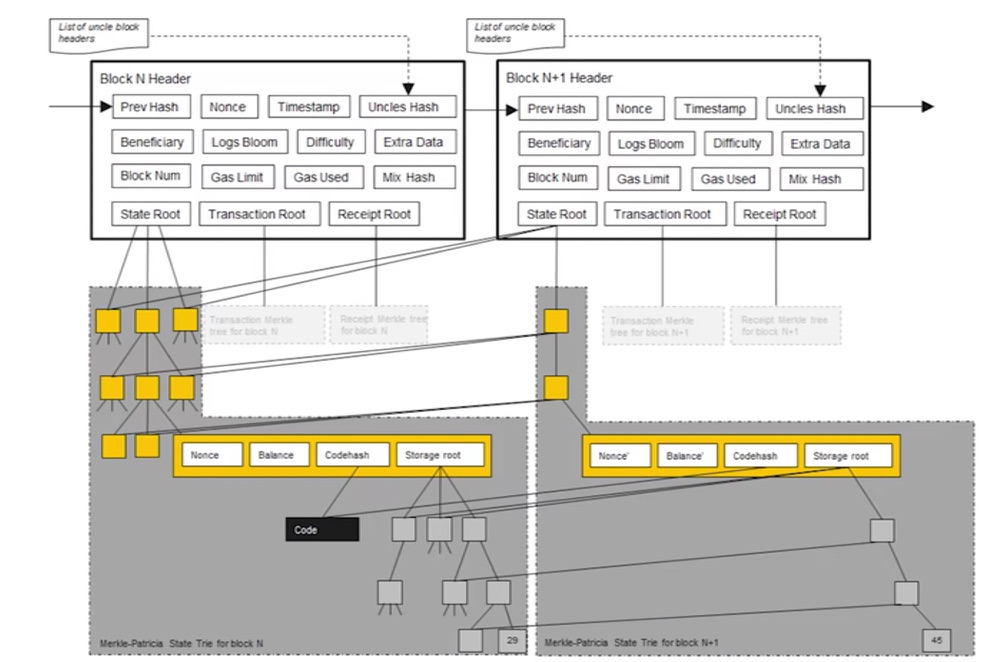
所以,系统中全节点并非维护一棵MPT,而是每次发布新区块都要新建MPT。只不过大部分节点共享。
为什么要保存原本状态?为何不直接修改? 为了便于回滚。如产生分叉后上面节点胜出,那么下面节点中状态的修改便需要进行回滚。因此,需要维护这些历史记录。
block header 中的数据结构

- Parenthash: 父区块的哈希(前一个区块的哈希)
- Unclehash: 叔父区块的哈希
- Coinbase: 矿工地址
- Root: 状态树的根哈希值
- Txhash: 交易树的根哈希值
- Receipthash: 收据树的根哈希值
- Bloom: 整个区块块头的 Bloom filter
- Difficulty: 挖矿难度
- GasLimit: 汽油费(类似于比特币中的交易费)相关
- GasUsed: 汽油费(类似于比特币中的交易费)相关
- Time: 区块产生时间
- Mixdigest: 挖矿过程随机数算出来的哈希值
- Nonce: 挖矿时随机数
区块结构

- header: 指向 block header 的指针
- uncles: 指向叔父区块的指针
- transactions: 交易列表
区块在网上真正发布时的信息
type extblock struct {
Header *Header
Txs []*Transactions
uncles []*Header
}
状态树中保存
Key-value对,key就是地址,而value状态通过RLP(Recursive Length Prefix,一种进行序列化的方法)编码序列号之后再进行存储。
# ETH 交易树和收据树
每次发布一个区块时,区块中的交易会形成一颗 Merkle Tree,即交易树。此外以太坊还添加了一个收据树,每个交易执行完之后形成一个收据,记录交易相关信息。交易树和收据树上的节点是一一对应的,且都是 MPT。MPT 的好处是支持查找操作,通过键值沿着树进行查找即可。
- 对于状态树,查找键值为账户地址。
- 对于交易树和收据树,查找键值为交易在发布的区块中的序号。
收据树作用:在以太坊中最重要的功能是加入了智能合约,而智能合约的执行过程比较复杂,收据树的作用是利于系统快速查询执行结果。
# 布隆过滤器(Bloom filter)
作用:布隆过滤器可以用于检索一个元素是否在一个集合中。它的优点是空间效率和查询时间都远远超过一般的算法,缺点是有一定的误识别率和删除困难。
给定一个数据集,其中含义元素
a、b、c,通过一个哈希函数H()对其进行计算,将其映射到一个其初始全为0的128位的向量的某个位置,将该位置置为1。将所有元素处理完,就可以得到一个向量,则称该向量为原集合的摘要。该摘要比原集合是要小很多的。 假定想要查询一个元素d是否在集合中,假设H(d)映射到向量中的位置处为0,说明d一定不在集合中;假设H(d)映射到向量中的位置处为1,可能集合中确实有d,也有可能因为哈希碰撞产生误报。 个人理解就是:他会告诉你某样东西一定不存在或者可能存在。
# Bloom filter 在以太坊中的应用
每个交易完成后会产生一个收据,收据包含一个 Bloom filter 记录交易类型、地址等信息。在区块 block header 中也包含一个Bloom filter,其为该区块中所有交易的 Bloom filter 的一个并集。
所以,查找时候先查找块头中的 Bloom filter,如果块头中包含。再查看区块中包含的交易的 Bloom filter,如果存在,再查看交易进行确认;如果不存在,则说明发生了 碰撞。
好处就是通过 Bloom filter 这样一个结构,快速大量过滤掉大量无关区块,从而提高了查找效率。
# 补充
以太坊对于给定的当前状态和给定一组交易可以确定性的转移到下一状态,这一运行过程可以视为交易驱动的状态机,通过执行当前区块中包含的交易,驱动系统从当前状态转移到下一状态。当然,BTC 我们也可以视为交易驱动的状态机,其状态为 UTXO。
问题1:A转账到B,有没有可能收款账户不包含再状态树中?
可能。因为以太坊中账户可以节点自己产生,只有在产生交易时才会被系统知道。 问题2:可否将每个区块中状态树更改为只包含和区块中交易相关的账户状态?(大幅削减状态树大小,且和交易树、收据树保持一致) 不能。首先,这样设计要查找账户状态很不方便,因为不存在某个区块包含所有状态。其次,如果要向一个新创建账户转账,因为需要知道收款账户的状态,才能给其添加金额,但由于其是新创建的账户,所有需要一直找到创世纪块才能知道该账户为新建账户。
# 代码实现
func NewBlock(header *Header, txs []*Transaction, uncles []*Header, receipts []*Receipt, hasher TrieHasher) *Block {
b := &Block{header: CopyHeader(header)}
// 交易列表是否为空
if len(txs) == 0 {
// 块头里的交易树的根哈希值为空哈希值
b.header.TxHash = EmptyTxsHash
} else {
// 调用 DeriveSha 获得根哈希值
b.header.TxHash = DeriveSha(Transactions(txs), hasher)
// 创建交易列表
b.transactions = make(Transactions, len(txs))
copy(b.transactions, txs)
}
// 收据列表是否为空
if len(receipts) == 0 {
// 块头里的收据树的根哈希值为空哈希值
b.header.ReceiptHash = EmptyReceiptsHash
} else {
// 调用 DeriveSha 获得根哈希值
b.header.ReceiptHash = DeriveSha(Receipts(receipts), hasher)
// 创建 Bloom Filter
// CreateBloom 函数用来创建 Block Header 中的 Bloom 域,
// 这个 Bloom Filter 由这个块中所有 receiptes 的 Bloom Filter 组合得到
b.header.Bloom = CreateBloom(receipts)
}
// 叔父列表是否为空
if len(uncles) == 0 {
// 块头里的叔父区块的哈希值为空哈希值
b.header.UncleHash = EmptyUncleHash
} else {
// 通过 CalcUncleHash 计算出哈希值
b.header.UncleHash = CalcUncleHash(uncles)
// 通过循环构造出叔父数组
b.uncles = make([]*Header, len(uncles))
for i := range uncles {
b.uncles[i] = CopyHeader(uncles[i])
}
}
return b
}
// DeriveSha 函数
func DeriveSha(list DerivableList) common.Hash {
keybuf := new(bytes.Buffer)
trie := new(trie.Trie)
for i := 0; i < list.Len(); i++ {
keybuf.Reset()
rlp.Encode(keybuf, uint(i))
trie.Update(keybuf.Bytes(), list.GetRlp(i))
}
return trie.Hash()
}
// 收据数据结构
type Receipt struct {
PostState []byte `json:"root"`
Status uint64 `json:"status"`
CumulativeGasUsed uint64 `json:"cumulativeGasUsed" gencodec:"required"`
Bloom Bloom `json:"logsBloom" gencodec:"required"`
Logs []*Log `json:"logs" gencodec:"required"`
TxHash common.Hash `json:"transactionHash" gencodec:"required"`
ContractAddress common.Address `json:"contractAddress"`
GasUsed uint64 `json:"gasUsed" gencodec:"required"`
}